图的遍历

1. 定义：

从图中某一个顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历。

2. 标记：

为了防止一个结点被多次访问，而其他结点没有被访问的情况。因此需要对访问过的结点打上标记，设置一个访问数组visited[n]，n是图中顶点的个数，初值为0，访问过后设置为1。

通常有两种遍历次序方案：深度优先遍历与广度优先遍历。

3. 深度优先遍历

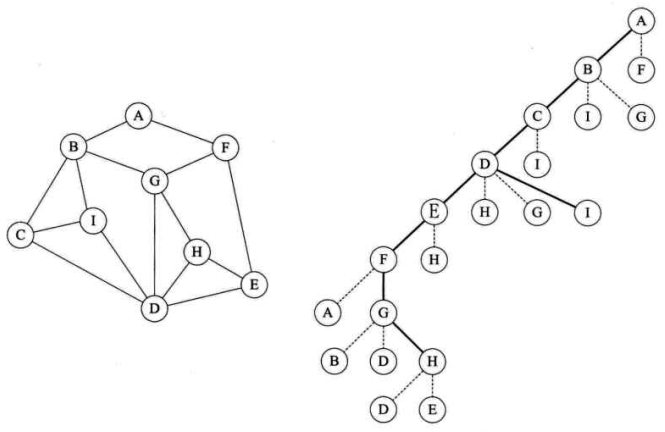
遍历过程：（类似于树的前序遍历）

【1】前进：从结点A出发，始终向右手边走（A的右手边是B），当右手边的结点是已经走过的结点时（标记过），退回上一个结点，选择次右结点。

【2】退回：一直到找到的某一个结点其相邻的所有结点都已经遍历。则执行退回操作。一直退回到最初的节点，终止。

A->B->C->D->E->F->A(已经遍历过)->F(退回到F)->G->B(已经遍历过)->G->D(已经遍历过)->G->H

注意此时结点并没有被全部遍历，执行回退操作

H(无通道没走过)->G(无通道没走过)->F(无通道没走过)->E(无通道没走过)->D->I(没有走过该通道)->D(无通道没走过)->C(无通道没走过)->B(无通道没走过)->A(返回最初顶点)

代码：(是一个递归过程)

使用邻接矩阵存储结构

使用邻接表存储

 

 

4. 广度优先遍历

 

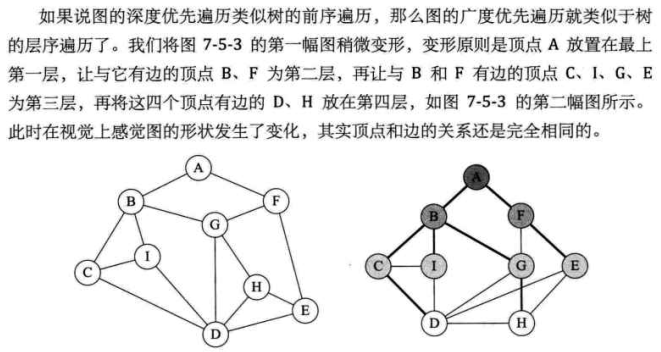
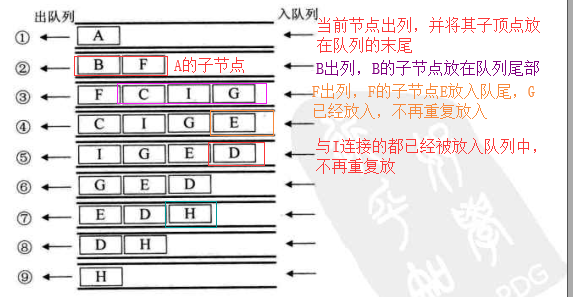
代码：

 使用邻接矩阵存储结构

 

使用邻接表存储

 

讨论;

图的深度优先遍历与广度优先遍历，时间复杂度是一样的，不同之处仅仅在于对顶点的访问顺序不同。

深度优先更适合目标比较明确，以找到目标为主要目的的情况，而广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。